MOVIMIENTO DE PROYECTILES O TIRO PARABÓLICO
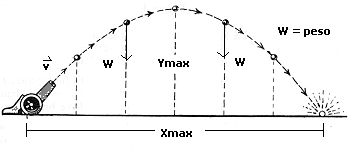
Cuando un objeto es lanzado al aire, éste sufre una aceleración debida al efecto del campo gravitacional. El movimiento más sencillo de éste tipo es la caída libre; pero cuando un cuerpo, además de desplazarse verticalmente, se desplaza horizontalmente, se dice que tiene un movimiento de proyectil, también conocido como movimiento parabólico, que es un caso más general de un cuerpo que se lanza libremente al campo gravitacional, y se trata de un movimiento bidimensional. Un objeto que se lanza al espacio sin fuerza de propulsión propia recibe el nombre de proyectil*.En éste movimiento, se desprecia el efecto de la resistencia del aire; entonces, el único efecto que un proyectil sufre en su movimiento es su peso, lo que le produce una aceleración constante igual al valor de la gravedad.
 |
 Ejemplo. Se dispara un proyectil de mortero con un ángulo de elevación de 30º y una velocidad inicial de 40 m/s sobre un terreno horizontal. Calcular:
Ejemplo. Se dispara un proyectil de mortero con un ángulo de elevación de 30º y una velocidad inicial de 40 m/s sobre un terreno horizontal. Calcular: a) El tiempo que tarda en llegar a la tierra; b) El alcance horizontal del proyectil.
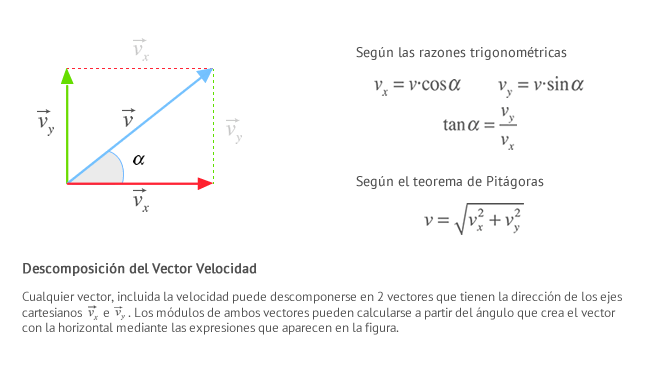
- Se tiene el valor de la magnitud de la velocidad inicial y el ángulo de elevación. A partir de ello, se pueden encontrar las componentes de la velocidad inicial y la velocidad final:
Vox = Vo cos θ = (40 m/s) cos (30º) = 34.64 m/s. (Ésta es constante)
Voy = Vo Sen θ = (40 m/s) sen (30º) = 20.0 m/s.
A. Si analizamos el tiempo en el que el proyectil tarda en llegar a la altura máxima, podemos encontrar el tiempo total del movimiento, debido a que es un movimiento parabólico completo. Suponga que tº es el tiempo en llegar a la altura máxima.
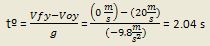
Como tº = t/2, donde t es el tiempo total del movimiento:
t = 2 * (2.04 s) = 4.08 s
B. El tiempo total del movimiento es el mismo tiempo en el que se obtiene el alcance horizontal. De M.R.U.:
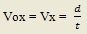
d = Xmax = Vx * t = (34.64 m/s) * (4.08 s) = 141.33 m
| LANZAMIENTO HORIZONTAL | |
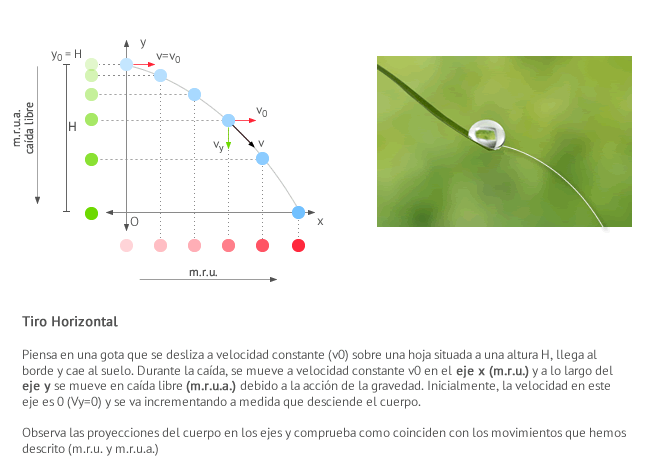
El lanzamiento horizontal consiste en lanzar un cuerpo horizontalmente desde cierta altura. En la siguiente figura puedes ver una representación de la situación:
 ALCANCE HORIZONTAL
ALCANCE HORIZONTAL
El alcance horizontal de cada uno de los proyectiles se obtiene para y=0.
Su valor máximo se obtiene para θ =45º, teniendo el mismo valor para θ =45+α , que para θ =45-α . Por ejemplo, tienen el mismo alcance los proyectiles disparados con ángulos de tiro de 30º y 60º, ya que sin(2·30)=sin(2·60).
La altura máxima que alcanza un proyectil se obtiene con vy=0.
Su valor máximo se obtiene para el ángulo de disparo θ =90º.
La envolvente de todas las trayectorias descritas por los proyectiles cuyo ángulo de disparo está comprendido entre 0 y 180º se denomina parábola de seguridad.
| LANZAMIENTO INCLINADO
Según Fundación Centro Nacional de Innovación Tecnológica:"Consiste en estudiar el caso de una partícula o proyectil que se lanza con una velocidad inicial, formando un ángulo con la dirección horizontal. Su velocidad cambia constantemente debido a la acción del campo gravitatorio" es decir, que estará presente dos movimientos en el lanzamiento, uno es, en el que el objeto sube hasta llegar a un punto máximo, y ahí se vuelve un lanzamiento de caída libre porque el objeto tendrá que bajar por causa de la gravedad.
|

ALTURA MÁXIMA
En tiro vertical, la altura máxima es el punto en el que el objeto alcanza su punto mas alto, en ese punto su energía cinética es cero, ya que no hay movimiento,su velocidad es V=0, pero su energía potencial mayor.
Recuerda que la energia potencial depende de la altura, osea, a mayor altura, mayor energía potencial.
Por ejemplo:Un cuerpo es lanzado verticalmente hacia arriba con una velocidad inicial a de 53m/seg .considera que la aceleración es de 10m/segundo cuadrado.
¿cuál es su altura máxima?
Rta: para esto usamos: h= Vf2 - Vo2 / -2g
entonces:
h= 0 m/s2 - 53 m/s2 / - (2) (10 m/s2)
queda:
0 m/s2 - 53 m/s2= -53
ahora: -53/-2 * 10= 265
h= 265m
La altura máxima que alcanzó el objeto fué de 265 m.
Por ejemplo:Un cuerpo es lanzado verticalmente hacia arriba con una velocidad inicial a de 53m/seg .considera que la aceleración es de 10m/segundo cuadrado.
¿cuál es su altura máxima?
Rta: para esto usamos: h= Vf2 - Vo2 / -2g
entonces:
h= 0 m/s2 - 53 m/s2 / - (2) (10 m/s2)
queda:
0 m/s2 - 53 m/s2= -53
ahora: -53/-2 * 10= 265
h= 265m
La altura máxima que alcanzó el objeto fué de 265 m.
TIEMPO DE VUELO
El tiempo de vuelo, en tiro parabólico, siempre que el piso sea horizontal, está dado por
t = 2 (vo/g) sen θ,
donde vo es la velocidad inicial, g la aceleración de la gravedad, y θ el ángulo de elevación, que es lo mismo que el ángulo que forma la velocidad inicial respecto a la horizontal.
Haciendo θ = 90° (o eliminando de la fórmula el término "sen θ"), también sirve para tiro vertical, indistintamente.
La fórmula se deduce de la fórmula general (para la componente vertical del movimiento):
h = vo t sen θ − ½ gt².
Para el tiempo en el que el proyectil vuelve a tocar tierra, h = 0, por lo que la fórmula se simplifica a
vo t sen θ = ½ gt²
vo sen θ = ½ gt
t = 2 (vo/g) sen θ.
t = 2 (vo/g) sen θ,
donde vo es la velocidad inicial, g la aceleración de la gravedad, y θ el ángulo de elevación, que es lo mismo que el ángulo que forma la velocidad inicial respecto a la horizontal.
Haciendo θ = 90° (o eliminando de la fórmula el término "sen θ"), también sirve para tiro vertical, indistintamente.
La fórmula se deduce de la fórmula general (para la componente vertical del movimiento):
h = vo t sen θ − ½ gt².
Para el tiempo en el que el proyectil vuelve a tocar tierra, h = 0, por lo que la fórmula se simplifica a
vo t sen θ = ½ gt²
vo sen θ = ½ gt
t = 2 (vo/g) sen θ.
CONCEPTOS FUNDAMENTALES
A. FRECUENCIA (f)
Es la razón que existe en la cantidad de vueltas en una ecuación matemática que se puede calcular un M.C.U
F = n/t = S-1 o Herzt
B. PERIODO (T)
Es la razon que existe entre el tiempo empleado en dar "n" vueltas, una ecuacion con la cual podamos calcular el M.C.U.
T = t/n = Segundos
C. VELOCIDAD LINEAL O TANGENCIAL (Vt)
Es un vector tangente a la trayectoria. Su magnitud se obtiene calculando el arco obtenido en la unidad de tiempo, es decir, " cuando la partícula da una vuelta completa, recorre una arco igual a la longitud de la circunferencia y emplea un tiempo igual a un periodo"
D. VELOCIDAD ANGULAR (W)
Esta tiene que ver con el angulo barrido en la unidad de tiempo. Lo que significa que es un vector perpendicular al plano lo que quiere decir, que sale o entra de acuerdo con el estudio de rotación del cuerpo.
W = Q/T = Rd/s
E. ACELERACIÓN CENTRIPETA (AC)
Aparece en un M.C.U, debido a la variación en la dirección de la velocidad.

LEYES DE NEWTON
Las leyes de Newton, también conocidas como leyes del movimiento de Newton, son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la mecánica, en particular aquellos relativos al movimiento de los cuerpos, que revolucionaron los conceptos básicos de la física y el movimiento de los cuerpos en el universo.
Constituyen los cimientos no solo de la dinámica clásica sino también de la física clásica en general. Aunque incluyen ciertas definiciones y en cierto sentido pueden verse como axiomas, Newton afirmó que estaban basadas en observaciones y experimentos cuantitativos; ciertamente no pueden derivarse a partir de otras relaciones más básicas. La demostración de su validez radica en sus predicciones. La validez de esas predicciones fue verificada en todos y cada uno de los casos durante más de dos siglos.

PRIMERA LEY DE NEWTON-LA INERCIA:
Esta indica que si un cuerpo dado no está sujeto a la acción de fuerzas, mantendrá sin cambio su velocidad (en magnitud y dirección). Esta propuesta se le debe originalmente a Galileo, pero Newton la adoptó como la primera de sus leyes para describir el movimiento de cuerpos.
A primera vista, esta ley parece ser menos compleja que las otras dos, pues carece de una expresión matemática y para colmo parece un corolario de su segunda ley (F = m a), pues la aceleración de un objeto es nula (o sea, su velocidad es constante) cuando no hay fuerzas actuando sobre él.El sentido original de la primera ley de Newton (conocida como Ley de la inercia), es que no se requieren fuerzas para mantener sin variación el movimiento de los cuerpos, sino solamente para cambiar la magnitud o la dirección de su velocidad. En otras palabras, no es necesario que haya una fuerza para que un cuerpo se encuentre en movimiento, sino únicamente para que cambie el estado del movimiento en sí. Este enunciado resultó fundamental cuando Galileo y Newton lo propusieron, pues según la percepción antigua y contradictoria a este principio, sustentada sobre todo un famoso libro de Aristóteles titulado precisamente Física, se requiere un "agente activo", o sea una fuerza, para mantener en movimiento un cuerpo, pues su "estado natural" es el de reposo.
EJEMPLOS:
1. El que al quitar un mantel rápidamente de una mesa, quedando puesto lo que se tenga arriba del mantel, es producto de la inercia.
2. Cuando corremos a alta velocidad nos cuesta más trabajo detenernos gracias a la inercia.
3. Cuando se empuja un auto que está en reposo, al principio cuesta trabajo debido a la inercia que se opone al movimiento, una vez que se empieza a mover es más fácil empujarlo, gracias a la inercia que tiene ahora en movimiento.
SEGUNDA LEY DE NEWTON-FUERZA O MOVIMIENTO:
La segunda ley de Newton creó un nuevo concepto, la fuerza, y ese nuevo concepto permitió entender los movimientos, por eso es conocida como la Ley del movimiento.
El movimiento tiene que ver con la sensación